My best planning. Part 3

Craig Barton interviewed me recently, during which I discussed a series of lessons I planned and taught on solving simultaneous equations.

I could be wrong, but I think this was the best planning and teaching I ever did.

Several people have asked if I would share examples of what I described during the interview, so I’m adding that here. It’s a bit lengthy, but hopefully provides the detail many people were asking for, as well as some insight into how Siegfried Engelmann’s Theory of Instruction can be applied to the classroom.

I’m splitting the post into four parts:

1. Specification of content
2. Sequencing of content
3. Pedagogy / Instructional Approach
4. Limitations of Atomisation

 

This is Part 3 – Pedagogy / Instructional Approach

***

Pedagogy / Instructional Approach

The choice of instructional approach varies depending on the type of concept being communicated, but in the podcast I talked about the sequence I used to teach addition and subtraction of equations, so I thought I’d share that in full here.

In this instance, the concept was treated as a Transformation, in Engelmann’s taxonomy.

My words for this sequence were scripted, most equations were chosen in advance, there was a single teacher example, and pupils responded to questions on mini-whiteboards.  There were 14 questions, and the whole sequence took around 20 minutes (I think it might have been possible to reduce the time used.)

My responses to what pupils wrote on their whiteboards were not scripted.  I wrote all equations up onto the whiteboard, and where minimal changes from one example to the next had been planned, I allowed pupils to watch me rub out the thing that had changed, and watch me input its replacement (e.g. changing a + sign to a – sign.)  This is referred to by Engelmann as Continuous Conversion, which I may write about separately at a later date.

Teacher Example

“In primary school you were taught how to add together numbers.  When you joined us in Year 7, we taught you how to add letters, unknowns, variables.  I’m now going to show you how to add together entire equations.  My turn first:”

The following was already written up onto the board as show.  I then proceeded to fill in the three boxes, in silence, with the numbers 7x, +10y, and 25.

I then paused for around 6-7 seconds, giving pupils reading and thinking time, before saying:

“Because 5x add 2x is 7x, 4y add 6y is +10y, and 20 add 5 is 25.”

Questions

“Your turn.  Add together the following two equations.  I only want to see the final result on your boards; what would go into the three boxes at the bottom.”

The following is the sequence of questions pupils were now asked to respond to.  I will add the intention at each stage, and whether it was designed to be minimally different from the previous example (apologies, some images have come out a little distorted.)  Although not shown here, each of these was set up the same as in my example above, with response boxes, until I state otherwise.  In every case, the response success rate was 80-100%, unless stated otherwise.

Identical to my example pair of equations, just with different numbers, still chosen for the arithmetic to be within everyone’s ability to compute mentally.

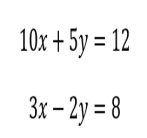
Minimally different, interleaving practice with simple negative arithmetic (5 add negative 2.)

Minimally different, intended to expose elimination of a variable as a possible consequence of adding two equations together.  Responses from pupils were a roughly even mixture of ‘0y’ and ‘     ‘  (blank space.)  We paused to discuss whether each was acceptable.

Back to the original set up.  Pupils were this time asked to subtract the second equation from the first.

Minimally different, intended to test whether pupils would correctly interleave a more complex negative arithmetic calculation with what they learnt (10 subtract negative 3.) Success rate dropped to ~70%, due to a variety of errors with this negative arithmetic.

Minimally different, but two changes made at the same time.  This was intended to test one of the most difficult negative arithmetic calculations (negative subtract negative,) at the same time as introducing the idea that elimination could occur through subtraction as well as addition.

Success rate dropped to ~50%, mostly involving errors around the negative arithmetic.  I regretted making two changes at once, especially where one was such an important concept, and the other was predictably going to result in many mistakes.

I opted to return to addition only for the rest of this sequence, and further develop that conceptualisation.

A return to our initial set up again, but with a single change designed to catch out lazy System 1 thinking.  About 50% success rate, but the failures all involved writing ’12x’ and ‘8y.’  When the mistake was pointed out, all of those pupils reacted in a way that suggested they immediately recognised their mistake, and wouldn’t make it so easily again!  (As opposed to not understanding why their response was incorrect.)

For this question, and future questions, the structure given by the response boxes was removed.

Minimally different, designed to test how pupils would respond to having an atypical set up, with no other x term to add.

Minimally different, designed to test how pupils would respond when there were no x or y terms to add.  This question added a layer of challenge, since the x and y terms presented were lined up.  This didn’t prevent the same typically high success rate as before, however (10x + 2y = 20,) which might hint that pupils learnt their lesson from the trap that was set two questions earlier.

Two new equations, intended to show that this addition concept was a feature of equations, not a feature of ‘letters,’ and to provide something concrete to show that the addition was producing true statements.

Pupils were asked not to simplify the left side of their equations after they added them, however many of the higher attaining pupils in the class did, responding with “25 = 25.”

Maximally different, designed to offer some significant challenge now, both by incorporating negative numbers again, and by removing the ‘set up’ that previous questions had enjoyed.  Pupils had to align these two for themselves, or else process them in their heads.

Maximally different.  Following our previous toying with changes to the variables presented, I wanted to test how pupils would respond when the variables were different in each equation (i.e. the equations are not simultaneous.)

To my surprise, the high success rate continued, with nearly every pupil responding with 10x + 5y + 2a + 3b = 20.

Minimally different.  This question was intended to push things even further, and test whether pupils returned ’13x’ on the left hand side.  I had reason to believe that they wouldn’t; up until now the inference they should have formed is ‘add the expressions on the left, then add the expressions on the right,’ but it is possible that some would generate a false inference – a misconception – upon seeing the x term return, and this would be an opportunity to correct that if so.

To my enduring surprise, every child bar one responded with “10x + 5y  + 2a + 3b = 20 + 3x.”

It took me a while to understand why one of the highest attainers had not got this right, to unpick her misconception (since she hadn’t written ’13x’,) until I finally realised that she had rearranged the equation, to return “7x + 5y + 2a + 3b = 20.”

I’m sure that should have been obvious, but you know what it can be like when under pressure in front of a class!

This was a final question, intended to apply the concept in one final new way, before wrapping up.  Again, the success rate was 100%.