My best planning. Part 1

Craig Barton interviewed me recently, during which I discussed a series of lessons I planned and taught on solving simultaneous equations.

I could be wrong, but I think this was the best planning and teaching I ever did.

Several people have asked if I would share examples of what I described during the interview, so I’m adding that here. It’s a bit lengthy, but hopefully provides the detail many people were asking for, as well as some insight into how Siegfried Engelmann’s Theory of Instruction can be applied to the classroom.

I’m splitting the post into four parts:

1. Specification of content
2. Sequencing of content
3. Pedagogy / Instructional Approach
4. Limitations of Atomisation

 

This is Part 1 – Specification of Content.

***

Context

Year 9, mixed prior attainment (no sets.)  The spread of prior attainment reached from what would be the ‘bottom set’ in most schools, to the ‘top set.’

9 hours of time spread across five lessons, to teach ‘solving simultaneous equations.’

I created this process, guided by Theory, but taught one out of three of the year 9 classes, and so much of the overview was co-planned with Lydia Povey, who taught the remaining Year 9 classes.  For this reason I will sometimes refer to ‘I,’ and sometimes refer to ‘we.’

Question 1

What’s the most difficult question type we would like all pupils to be able to respond to correctly, by the end?

Solve a pair of simultaneous equations, where both equations must be changed to provide a common coefficient for one of the variables.

e.g.

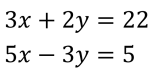
Solving by elimination will be covered, but substitution will not.

While needing to rearrange one or more of the equations is not stated explicitly here, it is an obvious additional step to include that would interleave prior content, and could therefore easily be incorporated into worksheets to challenge pupils – it is not, however, the 100% goal.

It might also be possible to touch on more than two equations and/or more than two variables during classroom practice, but again, this won’t be our measure of success.

Question 2

What are the sub-components of solving simultaneous equations that we should teach explicitly?

In this case, thirteen were identified:

1. Solve 1-Step equations
2. Substitute into x and y
3. Show that (x, y) is a solution to an equation
4. Identify when equations are unsolvable e.g. 3y+2x=10
5. Add / Subtract two or more equations
6. Identify when equations have an infinity of solutions e.g. 3y+2x=10
7. Find some solutions to an equation that has infinite solutions
8. Decide whether to add or subtract a pair of equations
9. Identify when equations have an infinity of solutions, from their graph
10. Determine whether a given value for (x, y) is a solution, based on the graph
11. Multiply two equations to get a common coefficient
12. Put everything together to solve a pair of simultaneous equation
13. Find the unique solution to a pair of simultaneous equations based on their graphs

The first three were recognised as having been covered in previous lessons, but were not assumed to be known by the pupils.

 

At the time, this felt pretty comprehensive.  Looking back at it now, I can see how it could be broken down much further.  For example, Identify whether two equations are simultaneous is an important component that was left out.

In The Myth of Ability, John Mighton explains how tutors learning to use his JUMP Math programme are often shocked by how many components a concept can be broken down into; what they used to consider ‘one step,’ it turns out, might be five.  Realising this, though, naturally invites the question: How far should we take it?  Should we break one idea into a hundred micro-pieces if we can?  Is more always better, or is there a trade off?

I’ll add some commentary on this in Part 4.

 

An important point to note:

Each of these is written in terms of a behaviour that we would expect to see a pupil exhibit.  Take Point 4 as an example.  This could be written ‘Know why some equations are unsolvable.’  This is superficially more desirable, since knowing *why* things are the way they are is obviously our end goal.  An implicit assumption is also often made: that if a pupil can express ‘why,’ then they should be able to apply that knowledge to the task of identifying equations that can’t be solved.  But… how do you assess whether a pupil really knows why…?  Ultimately, all we have are proxy measures, inferences we draw from behaviours that are actually observable.  A pupil might write an explanation as to ‘why’ quite convincingly, but perhaps they are just ‘regurgitating’ what they have been told, or copying and pasting what they read in the textbook…  This then leads to teachers feeling they have to withhold the why until the pupil ‘figures it out for themselves,’ introducing an extraordinary (I might offer, unacceptable) level of risk as to whether or not any given pupil will figure it out.  Then, even if successful, we still run into problems with transfer: a pupil who can articulate why quite eloquently still can’t necessarily solve related problems (e.g. the problem of identifying unsolvable equations.)

For these reasons, every single goal is expressed in terms of observable behaviours – if the pupil can do X, they have succeeded in learning what we intended to convey.

The bet being placed, here, is that ‘understanding’ and ‘why’ are functions of this web of related knowledge that is being slowly constructed, piece by piece.  We may screw that up by missing out important tasks or explanations in places, but that would mean those tasks or explanations simply need to be included so that the list of 13 concepts grows in size, rather than necessitating a change in approach.

That said, Point 4 was treated as one type of concept in Engelmann’s taxonomy that requires a follow up question, one which does ask for a ‘why.’  E.g.

Is this equation solvable?

– No.

How do you know?

– Because it has more than one unknown.

The explanation given here has been communicated to pupils directly, and the options available are very limited (either it has more than one unknown, or it doesn’t.)

This is not an exercise in reasoning; in Engelmann’s taxonomy, concepts of this type are ‘understood’ or recognised by their correlation with some other concept.  In this instance, solvable/unsolvable correlates with the number of unknowns in the equation:

Concepts of this kind are referred to by Engelmann as correlated-feature joining forms.

***

In Part 2 I’ll take a look at Question 3:

Question 3

How should we sequence this content over the time we have available?