*** UPDATE ***
On Tuesday 13th March, Ofsted announced the results of their visit to Charter.
**************
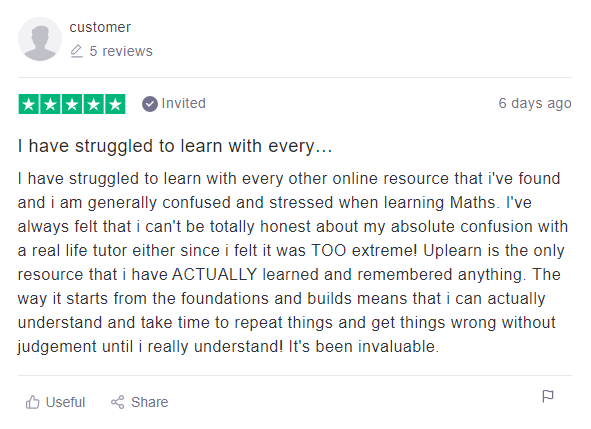
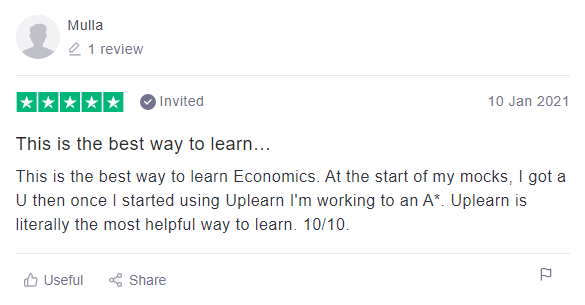
On Thursday I spent a morning at Great Yarmouth Charter Academy, and like many people, I’m angry.
Angry that there aren’t more schools like this, which was one of the most inspiring school environments I’ve seen.
Here’s what I saw:
- Everywhere teachers went, pupils greeting them with smiles and ‘good mornings’ that were heartwarming in their palpable sincerity
- Corridors that were calm, and orderly
- Behaviour in classrooms that was impeccable – amongst the best I have seen in any school, anywhere
- Every child I spoke to was grateful for any help I offered, obviously excited to learn more, and determined – I sat and worked with some children who repeatedly made mistakes, but were unperturbed and keen to keep going until they understood every mistake they made, and then continued into success; not a hint of wanting to give up
Many of the staff I spoke to had been there for over a decade. One had been there for fifteen years, and even went to the school as a pupil herself! After more than a decade of abuse and ingratitude, she was ready to pack it in this year, but now, she never wants to leave, and has never been happier.
This was a common theme. Teacher after teacher was joyful, welcoming, and said that they looked forward to coming into work every day – something that wasn’t true in the past.
One teacher said he couldn’t believe it: children who last year would swear at him every day, were now volunteering to hold the door for him, and wishing him a good day with a bright smile.
But what about the children?
Well, beyond what I’ve already said, I spoke with a Year 11 boy who achieved Grade 1 in his last mock exam, and recently achieved Grade 5.
I spoke with four Year 10 girls who told me that ‘everything’s changed’:
- At lunch, there would be an enormous queue waiting to be served, while people ran screaming around the lunch hall
- In the corridors pupils would be shouting and pushing people around
- Classes were 30 minutes long, they explained, not by design, but just that’s all that was left once everyone finally turned up
- Once there, no-one would learn because they were too busy using their rulers to fling the innards of glue sticks at one another, they said
But it’s not all good, they went on. They miss the ‘freedom they used to have.’
If they were in charge, I asked, would they make the decision to sacrifice that freedom to have what they have now?
They paused for several seconds to genuinely puzzle this one through, then offered a tentative, yes… yes it’s important to do well in school… followed by an effusive ‘yeah definitely, it’s much better now!’ – it was like watching the full realisation of the positive changes dawn on them.
One final Year 10 girl became the star of show, when she came over to tell me about her personal transformation. ‘Notorious,’ might be a word to describe her, ‘Every teacher knows who I am.’ She explained that she was in detention every day last year. This year, instead, she received at least one Golden Ticket every day, equivalent to three merits, and awarded to only one pupil per lesson. While she described herself as ‘loud,’ a more favourable estimation might describe her as ‘assertive;’ you could see her going far, if she could deliver the academic success, first. She was now averaging only a single demerit per week. She said she was finally learning; that she’d never learnt so much before.
This, again, was a common theme amongst pupils. Every pupil I asked insisted they had never learnt so much before, and they were all excited by it.
So is there anything to be ‘concerned’ about?
Were teachers shouting? Not that I heard – and given how settled the environment was, I think I would have if it were happening anywhere in the school.
Were pupils quivering in fear? I’m not sure I’ve ever seen happier children at school…
Were pupils being put in isolation for McDonald’s haircuts? Absolutely. And I was in awe at the warmth headteacher Barry Smith was able to radiate while sternly telling an apologetic Year 11 pupil that, after his exam, he would have to go straight to isolation. I wish I could do that, and the atmosphere of mutual respect was evident.
So throughout the day, when I thought about all the negative press I’d read, and the vitriol sprayed on Barry, I was angry.
It’s senseless.
But the other feeling I had today was hope.
Perhaps what stands out most at Charter is the feeling that… this is a pretty normal school. KSA, Reach, Michaela et al. they’re all exceptional schools, and have proved that ‘poor kids’ can be successful at school. But they’ve all done it with young, child-free teachers who regularly work 13 hour days, plus weekends – more than double the 1265 – to do ‘whatever it takes.’ (Albeit Michaela has tried to challenge that last one.)
Charter doesn’t have that. It’s staffed by a typical school workforce, and so for me what it feels closest to isn’t those schools that were the crucible of many of the ideas it implements, but my second school placement, Bishop Challoner in Birmingham, an outstanding school that benefits from a privileged intake. Unlike Charter, Bishop Challoner is not a school working in challenging circumstances, yet you’d struggle to tell the difference between the two.
So if they can do it at Great Yarmouth Charter Academy, if they can turn this school around and turn it into the next great success story, then it can be done anywhere.
And from what I’ve seen today, I believe they can, and they will.